Brillo absoluto

¿Es el Sol realmente la estrella más brillante del cielo? Supongamos que colocáramos todas las estrellas a la misma distancia de nosotros y luego midiéramos sus brillos. Así se obtendría la denominada magnitud absoluta. A pesar de haber eliminado el efecto de la distancia, todavía veríamos que las estrellas difieren bastante entre sí en cuanto a brillo.

En astronomía se define la magnitud absoluta de una estrella como la magnitud aparente que mostraría si se la colocara a una distancia de 10 pársecs, o 23.6 años luz. El sol brillaría con una magnitud absoluta +4.8, casi 10 magnitudes (10.000 veces) más débil que la estrella supergigante Betelgueuse cuya magnitud absoluta es -5.0.

Régulo (Regulus), la estrella blancoazulada en el extremo inferior derecho de Leo, muestra el mismo brillo aparente que la estrella anaranjada Algieba, situada en diagonal por encima de ella. Pero Régulo se halla al doble de distancia que Algieba. Parecen iguales por la sencilla razón de que Régulo posee una magnitud absoluta mucho más brillante.

Medir el brillo de las estrellas

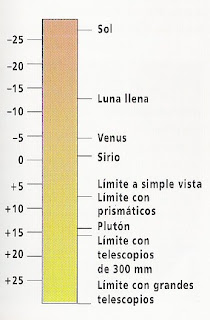
El sistema para medir el brillo de las estrellas data del siglo II a.C. y se debe al astrónomo griego Hiparco, que clasificó las estrellas más brillantes perceptibles a simple vista como de 1ª magnitud, y las más débiles como de 6ª magnitud.

El sistema de magnitudes actual se ha ampliado a objetos más débiles y más brillantes, pero la regla sigue siendo la misma: cuanto más débil sea un objeto, mayor es su magnitud. Los astros muy brillantes tienen magnitudes negativas. El Sol refulge con magnitud -26.8. La estrella más brillante del cielo nocturno, Sirio (Sirius), luce con magnitud -1.4. Vega tiene magnitud 0. Las estrellas del Carro tienen magnitud en torno a 2, mientras que los objetos más débiles que pueden detectarse con los grandes telescopios poseen magnitudes en torno a +30. Una diferencia de 5 magnitudes implica una diferencia de 100 veces en brillo.

Paralaje III

En 1835, el astrónomo alemán Johann Franz Encke (1791 - 1865) utilizó los datos relativos a los tránsitos de Venus para calcular la distancia del Sol, que resultó ser de 153.450.000 kilómetros. Esta cifra excedía un poco a la real pero sólo en algo más de tres millones de kilómetros.

La dificultad para obtener valores aún más exactos estribaba en que Venus y Marte aparecían en el ocular del telescopio como esferas diminutas, lo cual impedía fijar con precisión la posición del planeta. Venus era especialmente decepcionante en este aspecto, pues la espesa capa atmosférica que lo envuelve producía efectos ópticos que velaban ligeramente el momento exacto del contacto con el disco solar durante el tránsito.

Después sobrevino un acontecimiento inesperado. En 1801, el astrónomo italiano Giuseppe Piazzi (1746 - 1826) descubrió un pequeño planeta cuya órbita se hallaba entre Marte y Júpiter y lo bautizó con el nombre de Ceres. Este pequeño planeta resultó tener un diámetro algo inferior a 800 kilómetros. A medida que avanzó el siglo, se fueron descubriendo cientos de planetas aún menores, todos ellos girando entre las órbitas de Marte y Júpiter. Se trataba de los "asteroides". Más tarde, en 1898, el astrónomo alemán Karl Gustav Witt (1866 - 1946) descubrió Eros, un asteroide cuya trayectoria se alejaba de la "zona de los asteroides". Parte de su órbita pasaba por la de Marte, aproximándose bastante a la de la Tierra.

Estaba previsto que en 1931 Eros se acercaría a la Tierra a una distancia de unos 2/3la de Venus (que, de los grandes planetas, es el más cercano a la Tierra). Este acercamiento tan marcado significaba un paralaje nada común y fácilmente mensurable. Por otra parte, el tamaño de Eros es tan pequeño (se estima que su diámetro máximo es de unos 24 kilómetros), que no existía atmósfera alguna que pudiese difuminar sus contornos, con lo cual, y a pesar de su proximidad, el asteroide se observaría como un simple punto luminoso. De este modo podría determinarse su posición con gran exactitud.

Inmediatamente se organizó un vasto proyecto a escala internacional. Se estudiaron miles de fotografías, llegando por fin a la conclusión, a partir del paralaje y de la posición de Eros observados, que el Sol se encontraba a muy poco menos de 150.000.000 de kilómetros de la Tierra. Esta cifra es un promedio, pues nuestro planeta gira alrededor del Sol describiendo una elipse, no una circunferencia. La mínima distancia entre la Tierra y el Sol ("perihelio") es de 147.000.000 de kilómetros y la máxima ("afelio") de 152.200.000 kilómetros.

Paralaje II

Por desgracia, las condiciones que prevalecían hacia el año 1600 no permitían emplazar los observatorios a una distancia suficiente entre sí; esto, junto con la enorme distancia a que se hallaban los planetas, determinaba un desplazamiento aparente contra el fondo estrellado demasiado pequeño para ser susceptible de medidas precisas.

Años más tarde, en 1608, llegó el invento (o reinvento) del telescopio, debido al científico italiano Galileo Galilei (1564 - 1642). Este instrumento permitió aumentar los pequeños desplazamientos propios del paralaje, de suerte que una distancia angular imposible de detectar a simple vista se convertía, gracias al telescopio, en otra fácilmente mensurable.

Los planetas más cercanos (y por consiguiente aquellos cuyos paralajes eran mayores) eran Venus y Marte. Venus, sin embargo, pasa tan próximo al Sol en su posición de máximo acercamiento a este astro que resulta imposible observarlo (excepto en casos muy raros, cruzándolo en "tránsito"). Así pues, el objetivo lógico para la determinación del paralaje más allá de la Luna era el planeta Marte.

En 1671 se realizó la primera medida telescópica de calidad de un paralaje planetario. Uno de los observadores era Jean Richer (1630 - 1696), astrónomo francés que estuvo al frente de una expedición científica a Cayenne, en la Guayana francesa. El otro era el astrónomo ítalo-francés Giovanni Domenico Cassini (1625 - 1712), que permaneció en París. Ambos observaron el planeta Marte con la máxima simultaneidad posible y anotaron su posición respecto a las estrellas más próximas. Basándose en la diferencia de posiciones observada y en la distancia conocida de Cayenne a París, fue posible calcular la distancia de Marte en el momento del experimento.

Una vez efectuada esta medida, se disponía ya de la escala del modelo de Kepler, permitiendo así calcular todas las demás distancias del sistema solar. Cassini calculó, por ejemplo, que la distancia entre el Sol y la Tierra era de 140.000.000 de kilómetros, más de nueve millones de kilómetros inferior a la cifra real, pero resultado de todos modos excelente para ser el primer intento. La cifra de Cassini puede considerarse como la primera determinación útil de las dimensiones del sistema solar.

Durante los dos siglos que siguieron a los tiempos de Cassini se realizaron medidas algo más exactas de los paralajes planetarios. Algunas de ellas se referían a Venus, planeta que, en ciertas ocasiones, pasa justamente entre la Tierra y el Sol, apareciendo como un pequeño cuerpo circular oscuro que cruza el disco brillante del Sol. Tales "tránsitos" se registraron, por ejemplo, en 1761 y 1769. Si el tránsitos se observan desde distintos observatorios, se comprueba que tanto el momento en que Venus parece establecer contacto con el disco solar, como el momento en que se separa de éste y el tiempo que dura el tránsito, difieren de un observatorio a otro. Conocidas estas diferencias y las distancias entre los distintos observatorios, es posible calcular el paralaje de Venus; a partir de él, la distancia de este planeta, y desde aquí, la distancia del Sol.

Paralaje I

Para calcular la distancia de un cuerpo planetario antiguamente podía hacerso de un fenómeno conocido con el nombre de paralaje. Este fenómeno admite una ilustración muy simple, que consiste en colocar un dedo delante de los ojos contra un fondo que no sea uniforme. Manteniendo inmóviles la cabeza y el dedo y mirando alternativamente con un ojo y otro, se observa que la posición del dedo respecto al fondo varía. Acercando más el dedo a la cara las dos posiciones aparentes del dedo abarcarán una porción mayor del fondo.

Este efecto se debe a que entre los dos ojos existe una separación de varios centímetros, de modo que la línea imaginaria que une el dedo con uno de los ojos forma un ángulo apreciable con la que une el dedo con el otro. Si prolongamos ambas líneas hasta el fondo, resultarán sendos puntos que corresponden a las dos posiciones aparentes del dedo. Cuanto más próximo a los ojos coloquemos el dedo, mayor será el ángulo y mayor, por tanto, el desplazamiento aparente. Si los ojos estuvieran separados por una distancia mayor, aumentaría también el ángulo formado por las dos líneas, creando así un mayor desplazamiento aparente del dedo contra el fondo. (Por lo general, el fondo se encuentra tan alejado que un punto cualquiera sobre él forma con los dos ojos del observador un ángulo demasiado pequeño para poder medirlo. De ahí que el fondo pueda considerarse fijo.)

Este mismo principio cabe aplicarlo a un cuerpo celeste. Es cierto que la Luna se encuentra demasiado lejos para poder percibir alguna diferencia al mirar alternativamente con ambos ojos. Pero supongamos que observamos la Luna, contra el fondo estrellado del cielo, desde dos observatorios separados entre sí varios centenares de kilómetros. El primer observatorio verá que uno de los bordes de la Luna se halla a cierta distancia angular de una estrella concreta mientras que en ese mismo instante el segundo observatorio medirá entre el mismo borde y la misma estrella una distancia angular distinta.

Conocido el desplazamiento aparente de la Luna contra el fonde estrellado (suponiendo que las estrellas se hallan tan lejos que su posición permanece fija aunque varíe la situación del observatorio) y la distancia que media entre ambos observatorios, puede calcularse la distancia de la Luna con ayuda de la trigonometría.

Este experimento era perfectamente factible, pues el desplazamiento aparente de la Luna respecto a las estrellas al variar la posición del observador es bastante grande. Los astrónomos han normalizado dicho desplazamiento para el caso en que uno de los observadores vea la Luna en el horizonte y el otro justo encima de su cabeza. La base del triángulo es entonces igual al radio de la Tierra y el ángulo con vértice en la Luna es el "paralaje horizontal ecuatorial". Su valor observado es de 57,04 minutos de arco, o bien 0,95 grados de arco. Desplazamiento realmente apreciable, pues equivale a dos veces el diámetro aparente de la Luna llena. Se trata, por tanto, de una magnitud que se puede medir con suficiente precisión, permitiendo así obtener un buen valor para la distancia de la Luna. Esta distancia, calculada por la técnica del paralaje, concordaba bien con la cifra obtenida por ese antiguo método basado en la sombra proyectada por la Tierra durante un eclipse lunar.

Cómo medir el cielo

Para encontrar una estrella o un planeta hay que saber estimar posiciones en el cielo, así como familiarizarse con la escala astronómica de brillos. Una vez hecho esto, los datos de un anuario astronómicos, como por ejemplo, "Júpiter 5º, al norte de la Luna brilla con magnitud -2.5", dejan de parecer una jerga y se convierten en información útil. Las manos ofrecen un método sencillo para medir distancias en el cielo. Si se extiende el brazo por completo, el pulgar de la mano abarca 2 grados, un puño 10 grados, y la mano abierta del todo cubre 25 grados.

Muchos se preguntarán cómo describir el tamaño del Carro o su situación. En astronomía se utilizan grados angulares. Un ángulo de 90 grados (90º) cubre la distancia entre el horizonte y el cenit, que es el punto situado arriba en la vertical. Un ángulo de 45º nos lleva a media altura en el cielo. Si se abre la mano del todo con el brazo extendido, la distancia entre las puntas de los dedos meñique y pulgar cubre unos 25º. Este es también el tamaño del Carro, y sólo un poco menos de la distancia que media entre la estrella Polar y las dos estrellas del Carro que apuntan hacia ella.

El puño, con el brazo extendido, tiene 10 grados de anchura, mientras que el grosor del dedo pulgarcorresponde a unos 2 grados. Mucha gente piensa que la Luna tiene más o menos la anchura del pulgar, pero si se hace la prueba se constata que la Luna mide sólo medio grado, o 30 minutos de arco (30'). El ángulo más pequeño que se puede llegar a discernir (o resolver, en la terminología astronómica) a simple vista mide alrededor de un minuto de arco, o 60 segundos de arco (60''). El objeto más pequeño que puede resolverse con telescopios portátiles mide aproximadamente 1 segundo de arco (1'').

Nuestra costumbre de dividir la circunferencia en 360 grados la instauraron los babilonios en el tercer milenio a.C. Aquel pueblo usaba un sistema de numeración basado en el número 60, no en el 10, y veían en la circunferencia el símbolo del movimiento anual del Sol, que dura unos 360 días. Para ello era natural dividir el círculo en 360 grados, con cada grado dividido a su vez en 60 minutos. Seguimos usando el símbolo babilonio para el Sol (un pequeño círculo) como abreviatura de grado. El mismo principio se aplicó al concepto de día. Los babilonios lo dividían en 12 intervalos de una hora, cada uno de los cuales constaba de 60 minutos.

Cómo orientarse: el norte y el sur

El primer paso en cualquier paseo por las estrellas debe consistir en orientarse. Para interpretar las cartas celestes hay que saber dónde caen el norte y el sur. Los telescopios con montura ecuatorial deben alinearse con el polo celeste para que sigan correctamente las estrellas. En el hemisferio boreal basta buscar la estrella Polar (Polaris). La Polar no es el astro más refulgente del cielo, pero sí es la estrella brillante más cercana al polo norte celeste y, por tanto, marca la dirección del norte verdadero. El hemisferio austral carece de una estrella equivalente a la Polar, pero puede identificarse el rumbo sur si se usa la Cruz del Sur (Crux), que señala hacia el polo sur celeste.

En el hemisferio boreal hay que localizar el Carro de la Osa Mayor (Ursa Major). Después se traza la línea que une las dos estrellas del Carro más alejadas de la "lanza" (o "cola" de la osa). Al prolongar esa línea se llega a la estrella Polar (Polaris), junto al polo norte celeste.

En el hemisferio austral hay que localizar la Cruz del Sur (Crux), cuyo travesaño mayor apunta hacia el polo sur celeste, en una región vacía cercana a la estrella débil sigma Octantis. El polo cae a medio camino entre la Cruz del Sur y la brillante estrella Achernar, y forma un triángulo rectángulo con un astro aún más brillante, Canopo (Canopus). Una línea perpendicular a la que une alfa y beta Centauri también señalaría hacia el polo.

Los movimientos de las estrellas

Del mismo modo que la rotación de la Tierra desplaza el Sol a través del cielo cada día de este a oeste, también las estrellas que se ven de noche siguen ese mismo movimiento que las hace girar siempre alrededor del polo celeste. Además, a medida que la Tierra orbita en torno al Sol a lo largo del año, las constelaciones cambian con las estaciones.

La Tierra gira y, mientras lo hace, las estrellas salen por el horizonte oriental y se ponen en el occidental. Por ejemplo, en una tarde de diciembre podemos ver Orión alzándose por el este. Pero a medianoche está ya alto en el cielo, y lo vemos esconderse hacia poniente ya cerca del alba.

El cielo parece rotar alrededor de los dos polos celestes a medida que la Tierra gira. El movimiento concreto de las estrellas respecto del horizonte local depende del lugar de la Tierra desde el que se observe.

Si se observa desde un témpano de hielo en el polo norte, el polo norte celeste cae justo encima de la cabeza. El cielo gira alrededor de ese punto mientras la Tierra rota. Todas las estrellas trazan circunferencias paralelas al horizonte, sin salir ni ponerse. Desde el ecuador se observa el ecuador celeste que pasa por encima de la cabeza, en tanto que los dos polos celestes yacen el horizonte, uno al norte y otro al sur. El cielo rueda alrededor de esos dos puntos del horizonte y levanta las estrellas en vertical hacia el este, y las hace bajar rectas hacia el norte.

Entre ambos extremos, en las latitudes medias boreales, la esfera celeste se muestra inclinada. El polo norte celeste aparece a media altura en el cielo y las estrellas trazan círculos centrados en este punto estacionario. Desde la misma latitud pero en el hemisferio austral, las estrellas siguen moviéndose de este a oeste pero parecen girar alrededor del polo sur celeste, visible también a media altura.

El lado nocturno de la Tierra está orientado hacia partes diferentes del firmamento en las distintas posiciones que ocupan el planeta a medida que gira alrededor del Sol. Podemos compararlo con un gran tiovivo que nos arrastrara y nos ofreciera así, en cada momento, vistas distintas de un panorama lejano. En junio miramos hacia Sagitario, mientras que Orión se halla en dirección contraria, cerca del Sol y, por tanto, visible sólo de día. Seis meses más tarde, en diciembre, la cara nocturna de la Tierra mira hacia Orión, mientras que el Sol aparece en la dirección de Sagitario.

Unir los puntos

Las constelaciones no son más que figuras que trazamos en el cielo por pura conveniencia, enlazando una estrella con otra como un dibujo. Con escasas excepciones, las estrellas que forman una constelación no guardan relación entre sí en el espacio. Por ejemplo, Betelgueuse (la estrella que ocupa el hombro oriental de Orión) dista 427 años luz de la Tierra, mientras que Bellátrix (Bellatrix, el hombro occidental), está a medio camino, 243 años luz. Las estrellas del cinturón de Orión lucen a distancias de entre 800 y 900 años luz.

Si pudiéramos viajar hasta alejarnos cientos de años luz de la Tierra y contemplar las estrellas de Orión desde otro lugar de la Galaxia, no veríamos nada parecido a la figura humana que distinguimos desde la Tierra. Los extraterrestres de otros planetas verían figuras estelares muy distintas, aunque sus constelaciones incluyeran muchas de las estrellas que vemos desde aquí.

Constelaciones viejas y nuevas

El astrónomo griego Tolomeo enumeró, en el siglo II de nuestra era, un total de 48 constelaciones de fronteras difusas. Hoy dividimos el cielo en 88 constelaciones con límites precisos que siguen en zigzag la demarcación acordada oficialmente en 1930. Aunque las fronteras sean modernas, muchas constelaciones son tan antiguas como la misma civilización. Los antiguos sumerios, por ejemplo, ya representaban un león en la región del cielo donde aún vemos Leo, y un toro donde dibujamos ahora Tauro.

Otras constelaciones datan de los siglos XVII y XVIII. Algunas se introdujeron para cartografiar el cielo austral, desconocido para la astronomía europea antes de la era exploradora que se inició en el siglo XVI. Por ejemplo, la Cruz del Sur (Crux) la definió como constelación por primera vez Andrea Corsali, quien navegó a los trópicos con una expedición portuguesa en 1515.

Las constelaciones, países celestes

Podemos identificar cualquier lugar de la Tierra dando su posición en términos de longitud y latitud. Pero resulta más fácil imaginar la ubicación de una ciuad si la consideramos situada en un país concreto. Lo mismo ocurre con el cielo. La brillante estrella Betelgueuse o Betelgeuse tiene por coordenadas celestes 5 h 55.2 m de ascensión recta y +7º24' de declinación, pero ¿cómo recordarlo? En vez de recurrir a las coordenadas, decimos que Betelgueuse brilla en la constelación de Orión, el cazador.

Aprender a localizar alrededor de una docena de las constelaciones más brillantes supone una gran ayuda a la hora de orientarse en el cielo nocturno. De este modo, las estrellas dejan de parecer un caos de puntos inconexos y empiezan a organizarse en figuras conocidas.

Declinación y ascensión recta

Dibujemos en la esfera celeste líneas concéntricas paralelas al ecuador, centradas en los polos como los círculos de una diana. Al igual que las líneas de latitud en la Tierra, estos paralelos de declinación miden cuánto dista del ecuador, hace el norte o hacia el sur, cada lugar del cielo. Una estrella en el ecuador celeste tiene una declinación de 0 grados. Una estrella en el polo norte celeste tiene +90 grados de declinación, mientras que a una estrella a medio camino entre el ecuador y el polo le corresponden +45 grados. Un grado de declinación (º) contiene 60 minutos de arco (') y cada minuto de arco, a su vez, contiene 60 segundos de arco ('').

Tracemos ahora líneas en dirección norte-sur, de polo a polo. Igual que la longitud de la Tierra, estas líneas de ascensión recta miden la posición de las estrellas hacia el este o el oeste. El equivalente astronómico del meridiano terrestre de Greenwich, de longitud 0 grados, es el punto del ecuador celeste donde se halla el Sol cada año en el instante del equinoccio de marzo. La línea de ascensión recta que corta el ecuador celeste en ese punto tiene, por definición, 0 horas de ascensión recta.

El cielo está dividido en 24 horas (h) de ascensión recta, y cada una de ellas consta de 60 minutos de tiempo (m). Las horas crecen desde el oeste hacia el este.

La esfera celeste

Las posiciones de las estrellas y otros cuerpos celestes se determinan mediante un sistema de coordenadas dibujado a modo de rejilla sobre una esfera celeste imaginaria. La declinación y la ascensión recta se emplean del mismo modo que la latitud y la longitud terrestres. Como la Tierra, el cielo tiene un ecuador y dos polos. La eclíptica, un rasgo exclusivo del cielo, marca el recorrido aparente del Sol. La flecha roja señala el movimiento diurno aparente de la esfera hacia el oeste.

Aunque sabemos que la Tierra se mueve, en ocasiones resulta conveniente representar los cielos al modo de los antiguos, como si consistieran en una esfera cristalina que gira sobre nuestras cabezas, con los objetos astronómicos "pegados" en su superficie interna. La astronomía organiza esta esfera mediante una rejilla de coordenadas.

Imaginemos que atravesamos la Tierra, como si se tratara de un pollo asado, con un asta que entre por el polo sur del planeta, pase por el centro y surja por el polo norte. Prolonguemos mentalmente el asta en ambas direcciones de manera que se adentre en el espacio. En algún momento tocará nuestra esfera cristalina en dos puntos llamados polos celestes norte y sur. La esfera celeste entera parece girar alrededor de estos dos polos a medida que rota la Tierra.

Si expandimos ahora la línea del ecuador terrestre, como si fuera una cinta elástica gigante, acabará chocando con la esfera cristalina y trazando sobre ella el ecuador celeste, una línea imaginaria que secciona el cielo por la mitad en los hemisferios celestes boreal y austral, del mismo modo que el ecuador de la Tierra la divide a medio camino entre los polos.

La Luna en cuarto menguante

1 Albategnius
2 Alphonsus
3 Archimedes
4 Aristarchus
5 Clavius
6 Copernicus
7 Eratosthenes
8 Gassendi
9 Grimaldi
10 Hipparchus
11 Kepler
12 Mare Cognitum
13 Mare Frigoris
14 Mare Humorum
15 Mare Imbrium
16 Mare Nubium
17 Mare Vaporum
18 Montes Alpes
19 Montes Apenninus
20 Oceanus Procellarum
21 Plato
22 Ptolemaeus
23 Rupes Recta
24 Sinus Iridum
25 Tycho
26 Alunizaje de Apollo XII
27 Alunizaje de Apollo XIV
28 Alunizaje de Apollo XV

El hemisferio occidental de la Luna contiene Oceanus Procellarum, una gran extensión inundada de lava que conecta varios mares lunares. El cercano cráter de impacto Copernicus es el más destacado de toda la Luna. Tiene 93 kilómetros de diámetro y presenta barrancos en las murallas externas, terrazas hundidas en el interior y múltiples picos centrales formados por material procedente del subsuelo lunar. Copernicus está rodeado de un sistema de rayos formados por rocas esparcidas durante la formación del cráter hace unos 800 millones de años.

Al norte de Copernicus se encuentra Mare Imbrium, de 1160 km. El impacto que formó la cuenca Imbrium marcó gran parte del disco lunar, hace 3840 millones de caños. La lava que rellenó la cuencia es cientos de millones de años más reciente. La impresionante cordillera de los Apeninos lunares bordea parte de Mare Imbrium con montañas de más de 5000 m de altura. El Apollo XV aterrizó al pie de estas montañas en 1971.

Los Montes Alpes, cortados por el valle de los Alpes, contienen el cráter Plato, de 101 km, con el interior inundado de lava. Al oeste se divisa Sinus Iridum, un cráter de impacto de 260 km que perdió parte de sus murallas cuando las coladas de lava rellenaron la cuenca Imbrium.

Mare Humorum recuerda en parte a Mare Nectaris y posee cráteres parcialmente destruidos. El mejor rasgo que contiene en sus 425 km de diámetro es Gassendi, un cráter de 119 km inundado de lava y con el fondo surcado de fracturas. Las tierras altas del sur contienen Tycho, de 85 km, centro del mayor sistema de rayos de toda la Luna.

La Luna en cuarto creciente

1 Albatehnius
2 Aristóteles
3 Atlas
4 Endymion
5 Hércules
6 Hipparchus
7 Langrenus
8 Mare Crisium
9 Mare Fecunditatis
10 Mare Frigoris
11 Mare Nectaris
12 Mare Serenitatis
13 Mare Smythii
14 Mare Tranquilitatis
15 Mare Vaporum
16 Maurolycus
17 Montes Caucasus
18 Montes Taurus
19 Posidonius
20 Rupes Altai
21 Cresta Serpentina
22 Theophilus
23 Werner
24 Alunizaje de Apollo XI
25 Alunizaje de Apollo XVI
26 Alunizaje de Apollo XVII

El hemisferio oriental de la Luna contiene algunas cuencas de impacto rellenas de lava. Entre ellas se encuentra Mare Nectaris, una cuenca inundada sólo en parte y que aún muestra porciones de su borde elevado, la escarpadura Altai (Rupes Altai): los accidentes alcanzados por la lava muestran un aspecto suavizado y fundido. Mare Nectaris, de 860 km, yace al borde de las tierras altas, un tipo de terreno antiguo que cubre también la práctica totalidad de la cara oculta. Las tierras altas están tan craterizadas que cualquier impacto nuevo destruiría cráteres preexistentes.

Mare Serenitatis, de 920 km, es otra cuenca de impacto, pero en este caso se halla totalmente rellena de lava. La atraviesa la creata Serpentina, la mayor cresta arrugada de la Luna. Mide entre 100 y 200 m de latura y se formó cuando el peso de la lava deformó el fondo de la cuenca. La lava que inundó Serenitatis muestra colores diferentes, lo cual revela que surgió de varias erupciones distintas. El trazo claro que atraviesa el mar es un rayo procedente del cráter Tycho, situado cientos de kilómetros al suroeste.

Mare Crisium, de 740 km, parece alargado en sentido norte-sur debido a la perspectiva, pero en realidad está deformado de este a oeste. Esta cuenca de impacto aparece repleta de lava, si bien hay restos de una de sus murallas exteriores que demuestra que la cuenca Crisium tuvo el doble de tamaño recién formada.

El primer alunizaje (Apollo XI, 1969) se efectuó en Mare Tranqulitatis, mientras que el último (Apollo XVII, 1972) tuvo lugar en los Montes Taurus, en la costa sudeste de Serenitatis. Por desgracia, los módulos de alunizaje, banderas y huellas de las misiones Apollo son demasiado pequeños como para verlos desde la Tierra.